O governo de um estado pretende realizar uma obra de infraestrutura para auxiliar na integração e no processo de escoamento da produção agrícola de duas cidades. O projeto consiste na interligação direta das cidades A e B com a Rodovia 003, pela construção das Rodovias 001 e 002. As duas rodovias serão construídas em linha reta e deverão se conectar à Rodovia 003 em um mesmo ponto, conforme esboço apresentado na figura, na qual estão também indicadas as posições das cidades Ae B, considerando o eixo x posicionado sobre a Rodovia 003, e cinco localizações sugeridas para o ponto de conexão entre as três rodovias.
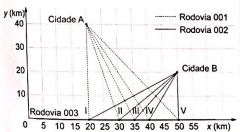
Pretende-se que a distância percorrida entre as duas cidades, pelas Rodovias 001 e 002, passando pelo ponto de conexão, seja a menor possível.
Dadas as exigências do projeto, qual das localizações sugeridas deve ser a escolhida para o ponto de conexão?
A) I
B) II
C) III
D) IV
E) V
Resolução:
A distância mais próxima entre dois pontos é uma linha reta (correto?). Assim, devemos fazer a projeção do ponto B (50,20) considerando o eixo X (Rodovia 003). Essa projeção resulta no ponto B' (50,-20).
Próxima fase é descobrir qual é o ponto P (x,0) no eixo X (Rodovia 003) que está alinhado com os pontos A (20,40) e B' (50,-20), utilizando o Determinante da Matriz Quadrada:
Esse método é explicado nesse link: https://www.todamateria.com.br/determinantes/
Pontos que devem estar alinhados:
A (20,40)
B' (50,-20)
P (x,0)
*Obs: o Ponto P tem a coordenada igual a zero uma vez que se encontra no eixo X. Em relação à abscissa, o valor de x é justamente o ponto que estamos querendo achar (ponto de interceptação da reta imaginária no eixo X).
Matriz a ser calculada:
20 40 1
50 -20 1
x 0 1
Resolução: a soma dos produtos das diagonais principais e secundárias tem que ser igual a zero para configurar o alinhamento (pontos pertencentes à mesma reta).
Sendo assim:
20*(-20)*1 + 40*1*x + 1*50*0 = x*(-20)*1 + 0*1*20 + 1*50*40
-400 + 40x = -20x + 2.000
60x = 2.400
x = 40
Ou seja, o ponto P calculado é P(40,0), que é exatamente a hipótese IV. (Alternativa D)
Nenhum comentário:
Postar um comentário