a) 120 cm; 50 cm e 130 cm.
b) 100 cm; 60 cm e 120 cm
c) 100 cm; 50 cm e 130 cm
d) 150 cm; 60 cm e 120 cm
e) 160 cm; 50 cm e 120 cm
Resolução:
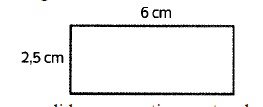
Como a figura está em uma escala de 1:20, para encontrarmos as medidas originais, basta multiplicar por 20 cada uma das medidas projetadas no desenho:
Comprimento => 6 . 20 = 120cm;
Largura (altura) => 2,5 . 20 = 50cm;
Note que a única alternativa que contém as duas medidas encontradas acima é a "A", ou seja, já temos nossa resposta. (Fique sempre atento a todos os detalhes de uma questão, pois como exemplificado acima, isso pode evitar cálculos desnecessários em situações em que o tempo é cronometrado para realização das questões - provas)
A título de aprendizado, vamos ainda sim, calcular a diagonal do retângulo. Para isso, vamos utilizar o Teorema de Pitágoras já que, uma diagonal pode dividir um retângulo em dois triângulos retângulos:
(Lembre-se que, em um triângulo retângulo, o quadrado da hipotenusa é igual a soma dos quadrados dos catetos)
Em nosso exercício, chamaremos de "d" a diagonal, que também é hipotenusa. Assim, teremos como catetos, o comprimento e a largura. Logo:
d² = 120² + 50²
d² = 14400 + 2500
d² = 16900
d = √16900
d = 130 cm
(alternativa A)
Nenhum comentário:
Postar um comentário