9(Enem - 2016) .Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.
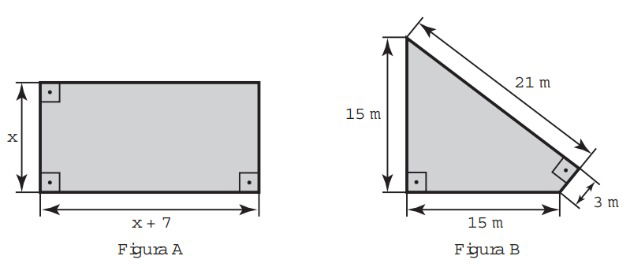
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
a) 7,5 e 14,5
b) 9,0 e 16,0
c) 9,3 e 16,3
d) 10,0 e 17,0
e) 13,5 e 20,5
Resolução:
Primeiramente, devemos calcular a área da figura B. Porém, é necessário dividi-la em duas partes para facilitar:
Assim, formamos então, dois triângulos. Calculando suas áreas temos:
Area1 = 15 x 15 / 2
Area 1 = 225 / 2
Area 1 = 112,5 m²
Area2 = 21 x 3 / 2
Area2 = 63 / 2
Area2 = 31,5 m²
Dessa forma, a Área da figura B será dada pela soma das duas áreas encontradas acima:
A_B = 112,5 + 31,5 = 144m²
Como a figura A é um retângulo, sua área será dada pelo produto das medidas do comprimento e altura, então:
A_A = x . (x + 7)
A_A = x² + 7x
Considerando que os dois terrenos devem ter a mesma medida, vamos então igualar os valore das áreas encontradas da figura A e B:
x² + 7x = 144m²
Resolvendo a equação de segundo grau temos:
x² + 7x - 144 = 0
Delta = 7² - 4 (1 . -144)
Delta = 49 + 576
Delta = 625
x' = - 7 + 25 / 2 => x' = 18/2 => x' = 9
x" = -7 - 25 /2 => x" = -32 /2 => x" = -16
Como se trata de medida vamos considerar apenas o valor positivo de "x", no caso o 9. Ciente do valor de "x" podemos então encontrar o valor das medidas da figura A:
x = 9;
x+7
9+7 = 16
Logo, o comprimento e a largura devem medir 9 e 16m (alternativa b)

Nenhum comentário:
Postar um comentário