10(Enem - 2015).O esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.

Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diferentes ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
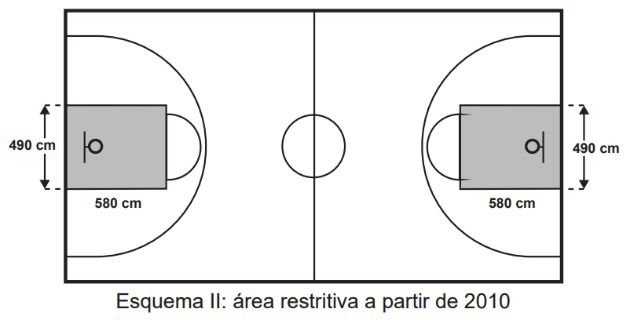
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
a) aumento de 5 800 cm2.
b) aumento de 75 400 cm2.
c) aumento de 214 600 cm2.
d) diminuição de 63 800 cm2.
e) diminuição de 272 600 cm2.
Resolução:
Devemos encontrar as áreas antes e depois da alteração. Primeiramente calculando a área trapezoidal do Esquema I temos:
A' = (B + b) h /2 (fórmula para cálculo da área do trapézio, onde B é a base maior, b é a base menor e h a altura)
A' = (600 + 360) . 580 / 2
A' = 960 . 580 / 2
A' = 556800 / 2
A' = 278400 cm²
Agora, devemos calcular a área retangular do Esquema II:
A" = b . h (fórmula para cálculo da área do retangulo, onde b é a base e h a altura)
A" = 580 . 490
A" = 284200 cm²
Por fim, fazendo a diferença entre as duas áreas temos:
A" - A' <=> 284200 - 278400 = 5800cm²
Logo, houve aumento de 5800cm² (alternativa A)
Nenhum comentário:
Postar um comentário